Use of GA-ANN and GA-SVM for a QSPR study on the aqueous solubility of pesticides Scientific paper
Main Article Content
Abstract
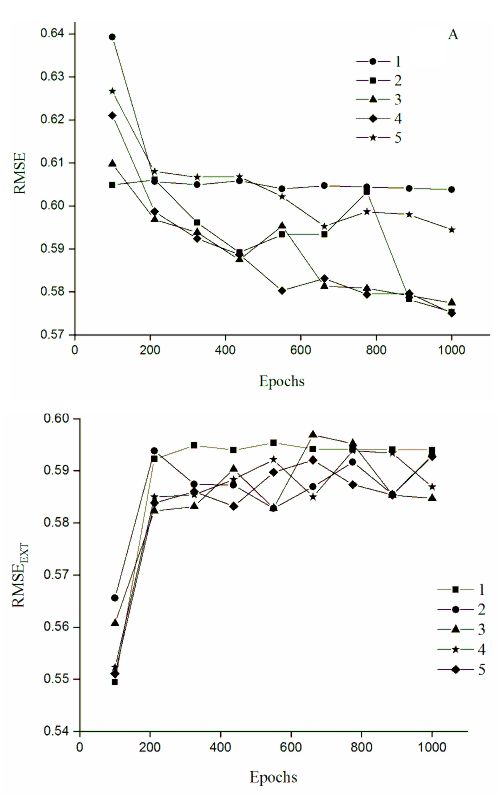
The partitioning tendency of pesticides, in this study herbicides in particular, into different environmental compartments depends mainly of the physicochemical properties of the pesticides itself. Aqueous solubility (S) indicates the tendency of a pesticide to be removed from soil by runoff or irrigation and to reach surface water. The experimental procedure for determining the aqueous solubility of pesticides is very expensive and difficult. QSPR methods are often used to estimate the aqueous solubility of herbicides. The artificial neural network (ANN) and support vector machine (SVM) methods, always associated with selection of a genetic algorithm (GA) of the most important variable, were used to develop QSPR models to predict the aqueous solubility of a series of 80 herbicides. The values of log S of the studied compounds were well correlated with the descriptors. Considering the pertinent descriptors, a Pearson correlation squared coefficient (R2) of 0.8 was obtained for the ANN model with a structure of 5-3-1 and 0.8 was obtained for the SVM model using the RBF function for the optimal parameters values: C = 11.12; σ = 0.1111 and ε = 0.222.
Downloads
Metrics
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution license 4.0 that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
References
P. Gramatica, A. Di Guardo, Chemosphere 47 (2002) 947 (https://doi.org/10.1016/S0045-6535(02)00007-3)
O. C. Hansen, Quantitative Structure–Activity Relationships (QSAR) and Pesticides, Pesticides Research No. 94, Teknologisk Institute, Taastrup, 2004 (https://www2.mst.dk/udgiv/publications/2004/87-7614-434-8/html/helepubl_eng.htm)
M. Zine, A. Bouakkadia, L. Lourici, D. Messadi, J. Serb. Chem. Soc. 84 (2019) 1405 (https://doi.org/10.2298/JSC190306059Z)
HyperchemTM, Release 6.03 for Windows, Molecular Modeling system, 2000 (http://www.hyper.com)
Molegro Data Modeller (MDM), v.2.0. Copyright Molegro (2009) (https://www.scientific-computing.com/press-releases/molegro-data-modeller-v20)
I. N. Levine, Quantum Chemistry. 5thed., Prentice Hall, Hoboken, NJ, 2000, pp. 626–739 (ISBN-10:0136855121)
R. Todeschini, V. Consonni, M. Pavan, Dragon, Software for the Calculation of Molecular Descriptors, Release 5.3 for windows, Milano, 2006 (http://www.talete.mi.it)
R. Todeschini, D. Ballabio, V. Consonni, A. Mauri, M. Pavan, MOBYDIGS, Software for Multilinear Regression Analysis and Variable Subset Selection by Genetic Algorithm, Release 1.1 for Windows, Milano, 2009 (http://www.talete.mi.it/)
R. Amiri, D. Messadi, A. Bouakkadia, J. Serb. Chem. Soc. 85 (2020) 467 (https://doi.org/10.2298/JSC190610090A)
D. E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, Addison Wesley, London, 1989, pp. 89–94 (https://dl.acm.org/citation.cfm?id=534133)
A. Beheshti, E. Pourbasheer, M. Nekoei, S. Vahdani, J. Saudi Chem. Soc. 28 (2016) 282 (http://dx.doi.org/10.1016/j.jscs.2012.07.019)
J. Xu, H. Zhang, L. Wang, G. Liang, L. Wang, X. Shen, W. Xu, Spectrochim. Acta, A 76 (2010) 239 (https://doi.org/10.1016/j.saa.2010.03.027)
S. Jothilakshmi, V. N. Gudivada, Handbook of Statistics, Vol. 35, Ch. 10, Elsevier, Amsterdam, 2016, pp. 301–340 (http://dx.doi.org/10.1016/bs.host.2016.07.005)
M. Safamirzaei, H. Modarress, M. Mohsen-Nia, Fluid Phase Equilib. 266 (2008) 187 (https://doi.org/10.1016/j.fluid.2008.01.022)
S. Haykin, Neural Networks: A Comprehensive Foundation, Prentice-Hall, New Delhi, 2006 (ISBN-13: 978-0023527616)
R. Rojas, Neural Network, Springer-Verlag, Berlin, 1996, pp. 229–261 (http://page.mi.fu-berlin.de/rojas/neural/)
O. Deeb, M. Drabh, Chem. Biol. Drug. Des. 76 (2010) 255 (https://dx.doi.org/10.4236/aces.2012.21010)
V. N. Vapnik, Statistical Learning Theory, John Wiley & Sons, New York,1998, pp. 375–473 (ISBN: 978-0-471-03003-4)
V. N. Vapnik, The Nature of Statistical Learning Theory. Springer, New York, 2000, pp. 267–287 (ISBN: 978-1-4757-3264-1)
C. J. Lu, T. S. Lee, C. C. Chiu, Decision Support. Syst. 47 (2009) 115 (https://doi.org/10.1016/j.dss.2009.02.001)
N. Cristianini, J. Shawe-Taylor, An introduction to support vector machines and other kernel- based learning methods, Publishing House of Electronics Industry, Beijing, 2005, pp. 93–122 (ISBN: 0521 780195).
R. Amiri, D. Messadi, A. Bouakkadia, L. Lourici, Egypt. J. Chem. 62 (2019) 1563 (https://doi.org/ 10.21608/ejchem.2019.4976.1446)
V. Vapnik, The Nature of Statistical Learning Theory, Springer, New York, 1995, pp. 70–71 (ISBN: 0-387-94559-8).
N. Cristianini, J. Shawe-Taylor, An Introduction to Support Vector Machines, Cambridge University Press, Cambridge, 2000, pp. 32–42 (ISBN: 0-521-78019-5).
B. Scholkopf, A. Smola, Learning with Kernels, MIT Press, Cambridge, MA, 2002, pp. 13–17 (ISBN: 0262194759)
A. Golbraikh, A. Tropsha, J. Mol. Graph. Model. 20 (2002) 269 (https://doi.org/10.1016/S1093-3263(01)00123-1)
N. Kertiou, A. Bouakkadia, D. Messadi, Res. J. Pharm. Biol. Chem. Sci. 8 (2017) 251 (https://www.rjpbcs.com/pdf/2017_8(6)/[29].pdf)
A. Bouakkadia,Y. Driouche, N. Kertiou, D. Messadi, Int. J. Saf. Secur. Eng. 10 (2020) 389 (https://doi.org/10.18280/IJSSE.100311)
A. Bouakkadia, H. Haddag, N. Bouarra, D. Messadi, Synthèse: Revue Sci. Technol. 32 (2016) 12 (https://www.ajol.info/index.php/srst/issue/view/13942)
J. Gasteiger, J. Sadowski, J. Schuur, P. Selzer, L. Steinhauer, V. Steinhauer, J. Chem. Inf. Comput. Sci. 36 (1996) 1030 (https://doi.org/10.1021/CI960343+)
J. Schuur, P. Selzer, J. Gasteiger, J. Chem. Inf. Comput. Sci. 36 (1996) 334 (https://doi.org/10.1021/CI950164C)
W. J. Wang, Z. B. Xu, W. Z. Lu, X. Y. Zhang, Neurocomputing 55 (2003) 643 (https://doi.org/10.1016/S0925-2312(02)00632-X)
O. Deeb, M. Goodarzi, Mol. Phys. 108 (2010) 181 (https://doi.org/10.1080/00268971003604575).